LOJ 2882. 「JOISC 2014 Day4」两个人的星座

对于任意两个凸多边形相离，一定可以找到一条直线将它们分在平面的两个区域

而对于三角形的情况更为特殊

分析可以发现，很难直接枚举三角形外直线计算，而对于任意的两个合法的三角形，在其6点中较近的4个点中

一定可以从两个三角形中各选一个点，连出两条交错的合法的分界线，例如下图

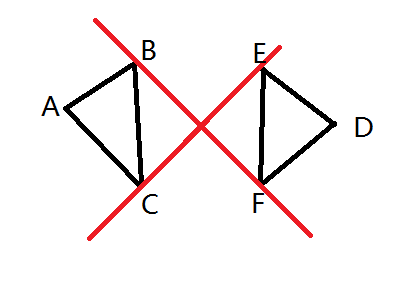
QQ截图20201102153211.png

那么可以考虑枚举这样的一条直线，即确定了两个分界线上的端点，然后从两个半平面内选出不同颜色的点

直接枚举，然后$O(n)$数出这样的点，复杂度为$O(n^3)$

显然可以想到枚举一个顶点，然后对于其他极角排序，旋转另一个点，同步统计半平面内的点个数，复杂度为$O(n^2\log n)$

实现上，可以枚举一个点，尺取一个半平面内的点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
using namespace std;
using ll=int64_t;
enum{N=3010};
int n,X[N],Y[N],I[N],C[N],c,s[2][3],i;
double T[N];
ll ans;
ll E(int j,int k){ return 1ll*(X[j]-X[i])*(Y[k]-Y[i])-1ll*(Y[j]-Y[i])*(X[k]-X[i]); }

int main(){
	for(int i=scanf("%d",&n);i<=n;++i) scanf("%d%d%d",X+i,Y+i,C+i);
	for(i=1;i<=n;++i) {
		c=0;
		memset(s,0,sizeof s);
		for(int j=1;j<=n;++j) if(i!=j) I[++c]=j,T[j]=atan2(Y[j]-Y[i],X[j]-X[i]),s[0][C[j]]++;
		sort(I+1,I+n,[&](int x,int y){ return T[x]<T[y]; });
		int p=1;
		for(int j=1;j<n;++j) {
			while(E(I[j],I[p])>=0) {
				s[0][C[I[p]]]--,s[1][C[I[p]]]++;
				p=p%c+1;
				if(p==j) break;
			}
			ans+=1ll*s[0][(C[i]+1)%3]*s[0][(C[i]+2)%3]*s[1][(C[I[j]]+1)%3]*s[1][(C[I[j]]+2)%3];
			s[1][C[I[j]]]--,s[0][C[I[j]]]++;
		}
	}
	cout<<ans/2;
}

一个更好的写法是把在$y$轴以下的点中心对称上来，统计时每跨过一个点改变一次 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;
enum{N=3010};
int n,X[N],Y[N],C[N],c,s[2][3],i,j,d,a,b,x,y;
int64_t ans;
struct Node{
	int x,y,d,c;
	Node(){ }
	Node(int p,int q,int r) {
		x=p,y=q,c=r,d=0;
		if(y<0||(x<0&&y==0)) d=1,x=-x,y=-y; 
		s[d][c]++;
	}
} A[N];
struct cmp{ int operator () (const Node &a,const Node &b){ return 1ll*a.x*b.y<1ll*a.y*b.x; } };
int main(){
	for(i=scanf("%d",&n);i<=n;++i) scanf("%d%d%d",X+i,Y+i,C+i);
	for(i=1;i<=n;++i) {
		memset(s,c=0,sizeof s),a=(C[i]+1)%3,b=(a+1)%3;
		for(j=1;j<=n;++j) if(i!=j) A[++c]=Node(X[j]-X[i],Y[j]-Y[i],C[j]);
		for(sort(A+1,A+n,cmp()),j=1;j<n;++j) {
			s[A[j].d][c=A[j].c]--,x=(c+1)%3,y=(x+1)%3;
			for(d=0;d<2;++d) ans+=1ll*s[d][a]*s[d][b]*s[!d][x]*s[!d][y];
			s[!A[j].d][c]++;
		}
	}
	cout<<ans/4;
}