「2020联考北附1」命运歧途

排列$dp$问题通常想到容斥，因为很难在$dp$的同时保证排列元素不多次出现

对于这个问题，我们只需要考虑相邻关系

我们需要计算包含0个非法位置的排列个数，因此容斥容易定义为计算

包含至少$i$个非法位置的排列个数，容斥系数可以简单设置为$(-1)^i$

考虑一个序列的合法与非法情况，容易发现是类似下面的情况

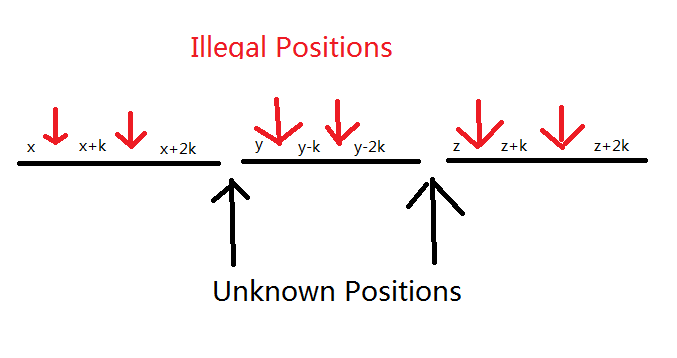
Snipaste_2020-11-30_19-31-05.png

序列会被分成若干段，每一段是形如$x,x+k,x+2k,\cdots$或者$x,x-k,x-2k$

显然$x,y$会产生非法关系的必要条件是$x\equiv t \pmod k$，因此按照$x\mod k$分组

组内实际上是类似$k=1$的子问题，不妨设一组包含$m$个元素

显然不同组之间一定构成不同的段，而对于一组内的元素，我们可以强制某一些位置分段

最终会得到一个若干段的序列，段之间由于不确定相互关系，设最终分成$i$段，则可以有$i!$种段之间排列

(分成$i$段的贡献在我们计算时实际上是至少包含了$n-i$个非法位置)

现在问题就是落到了$dp$序列分成$i$段的方案数，显然对于每一组，是一个分组背包的问题

对于每一个大小为$m$的组，考虑$dp$其分段方案

令$dp_{i,j}$表示当前已经确定的总大小为$i$且已经分成了$j$段

转移可以枚举下一段的大小$k$，由于实际排列中的段是有递增和递减两种情况，因此对于任意$k>1$，有两种段分配方法

转移式子是

$dp_{i,j}\rightarrow dp_{i+k,j+1} (k=1)$

$2dp_{i,j}\rightarrow dp_{i+k,j+1} (k>1)$

这个式子容易用前缀和优化，特殊的转移位置只有一个，处理一下即可

于是可以在$O(n^2)$复杂度内计算任何一个大小的组的分段方案

暴力合并组之间的背包，对于每个查询，复杂度为$O(n^2)$

因此总复杂度受限于查询，为$O(qn^2)$

接下来考虑如何削减查询复杂度

由于$q$的上限实际是$n$，下文认为$q=n$

优化1

上面的问题中，我们并没有具体地分析分组的情况

实际上对于$n,k$，可能的组大小只有两种，即$\lfloor \frac{n} {k}\rfloor ,\lceil \frac{n} {k}\rceil$

不同的$\lfloor \frac{n} {k}\rfloor $只有$O(\sqrt n)$种，不妨对于每种$\lfloor \frac{n} {k}\rfloor $从小到大计算每一个$k$的答案

简单观察即可发现：

在每个块内，按照$k$递增，两种组的个数一个递增一个递减

如果在每个$\lfloor \frac{n} {k}\rfloor $中，为最小的$k$暴力$O(n^2)$预处理出答案，然后不断增大

不妨维护两个单调的个数指针

如果能够支持背包回撤一个分组，增加一个分组，那么容易做到每个块内$O(n^2)$递推答案

增加一个分组不必说，而对于去掉一个分组，不好求出模逆元

但是由于上面的$dp_{i,j}$满足$dp_{i,i}=1$，因此考虑从高到低递推每一位

模拟一个长除法即可

合理的常数优化也可以通过此题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
const int N=2010;

int n,m,P;
int C[N][N],J[N];
int dp[N][N],S[N],F[N],G[N];

int len;
int pl=-1,nc1,nc2;
void clear() { 
	rep(i,0,len) F[i]=0;
	F[len=0]=1,nc1=nc2=0; 
}
int cnt=0;
void Mul(int m,int *A){ 
	drep(i,len+=m,0) {
		ull t=0;
		rep(j,1,min(i,m)) {
			t+=1ll*F[i-j]*A[j];
			((j&15)==0) && (t%=P);
		}
		F[i]=t%P;
	}
}
void Div(int m,int *A){ 
	static int G[N];
	rep(i,0,len) G[i]=F[i],F[i]=0;
	drep(i,len-=m,0) {
		ull t=G[i+m];
		rep(j,1,m) {
			t+=1ll*F[i+j]*(P-A[m-j]);
			((j&15)==0) && (t%=P);
		}
		F[i]=t%P;
	}
}

int Ans[N],Pow1[N],Pow2[N];
int clr;
void Solve(int m) {
	int l=(n-1)/m+1,c1=0,c2=0;
	rep(i,1,m) if((n-i)/m+1==l) c1++;
	else c2++;
	if(l==2) {
		rep(i,0,c1+c2) F[i]=0;
		rep(i,0,n-c1-c2) F[i+c1+c2]=1ll*C[c1][i]*Pow1[c1-i]%P*Pow2[i]%P;
		int x=1;
		rep(i,1,c2) x=1ll*x*dp[1][1]%P;
		rep(i,c1+c2,n) F[i]=1ll*F[i]*x%P;
	} else {
		if(l!=pl) {
			clr++;
			clear(); 
			pl=l;
		}
		cnt++;
		while(c1<nc1) Div(l,dp[l]),nc1--;
		while(c2<nc2) Div(l-1,dp[l-1]),nc2--;
		while(c1>nc1) Mul(l,dp[l]),nc1++;
		while(c2>nc2) Mul(l-1,dp[l-1]),nc2++;
	}
	rep(i,0,n) G[n-i]=1ll*F[i]*J[i]%P;
	int ans=0;
	rep(i,0,n) ans=(ans+1ll*((i&1)?-1:1)*G[i])%P;
	ans=(ans%P+P)%P;
	Ans[m]=ans;
}

int main() {
	freopen("fate.in","r",stdin),freopen("fate.out","w",stdout);
	n=rd(),m=rd(),P=rd();
	rep(i,0,n) rep(j,C[i][0]=1,i) C[i][j]=(C[i-1][j-1]+C[i-1][j])%P;
	rep(i,J[0]=1,n) J[i]=1ll*J[i-1]*i%P;
	dp[0][0]=S[0]=1;
	rep(i,1,n) {
		drep(j,i,1) {
			dp[i][j]=(2ll*S[j-1]+P-dp[i-1][j-1])%P;
			S[j]+=dp[i][j],Mod1(S[j]);
		}
	}
	rep(i,Pow1[0]=1,n) Pow1[i]=1ll*Pow1[i-1]*dp[2][1]%P;
	rep(i,Pow2[0]=1,n) Pow2[i]=1ll*Pow2[i-1]*dp[2][2]%P;
	rep(i,1,n-1) Solve(i);
	Ans[n]=J[n];
	fprintf(stderr,"%d %d\n",cnt,clr);
	rep(i,1,m) printf("%d\n",Ans[rd()]);
}

优化2

从生成函数的角度，我们容易把所求的值归纳为

$H(x)=F^a(x)G^b(x)$

我们知道多项式快速幂的复杂度为$\exp$的$n\log n$

当然那是对于长度为$n$的情况

而现在是长度之和为$n$

由于EI在无数道题中介绍了这个东西，看到马上想到可以求导

$H’(x)=aF^{a-1}(x)F’(x)G(x)+bG^{b-1}(x)G’(x)F(x)$

$H’=H(a\cdot \frac{F’} {F}+b\cdot \frac{G’} {G})$

理想的情况是：对于这个式子，两边从低到高解方程确定每一项的值

然而首先遇到的多项式除法操作就难以解决

要除掉的$F,G$没有常数项，而第一项系数为1或2，因此除法操作只需要计算$2$的逆元

因此可以考虑对于模数中的$2^t$提取出来，然后最后暴力exCRT合并

接下来就是分成两部分

计算$\mod 2^t$

由上面知道，背包的每一个位置实际对于最后答案的贡献是$i!(-1)^{n-i}$

因此对于$i!\mod 2^t=0$的位置都不用考虑，只需要求出背包前$O(\log P)$位，暴力即可

计算$\mod P(2\not |P)$

接下来就是上面的递推过程

然而还有一个问题就是从$[x^n]H’$得到$[x^{n+1}]H$，显然这里需要一个逆元

EI为我们提供一个很好的思路，或许有助于解决任意模数的逆元问题：

因为答案计算的是$k![x^k]H$，因此可以直接在计算过程中加入

这样求导的系数在阶乘中被省略，变成了单纯的平移

而乘法只需要额外添加一个权值$\binom{i+j} {i}\cdot x^i\cdot x^j\rightarrow x^{i+j}$

接下来具体的方法是：

先将$F(x),G(x)$平移一位去掉空余的项，处理过后$H(x)$被平移了$a+b$的位置，首项为$x^0$

从低到高递推$H(x)$的每一位，同步维护$ \frac{H} {F},\frac{H} {G}$

对于$H’(x)$的第$i$项累和得到，然后平移一位得到$H(x)$的$i+1$项

最后需要加上平移部分的贡献，$i!\rightarrow (i+a+b)!$，可以用一个组合数解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
const int N=2010;

int n,m,P;
int J[N];
int dp[N][N],S[N],F[N],G[N];

struct Solve2t{
	int F[N],P,U;
	void Init(int x) {
		P=x;
		int t=1;
		rep(i,1,n) {
			t=1ll*t*i%P;
			if(t==0) break;
			U=i;
		}
	}
	int Solve(int m) {
		rep(i,0,U) F[i]=0;
		F[0]=1;
		rep(x,1,m) {
			int c=(n-x)/m+1;
			rep(i,0,U) G[i]=F[i],F[i]=0;
			rep(i,0,U) if(G[i]) rep(j,1,min(c,U)) F[i+j]=(F[i+j]+1ll*G[i]*dp[c][j])%P;
		}
		int ans=0;
		rep(i,1,U) {
			F[i]=1ll*F[i]*J[i]%P;
			ans=(ans+(((n-i)&1)?-1:1)*F[i])%P;
		}
		ans=(ans%P+P)%P;
		return ans;
	}
} Sol1;

void Exgcd(ll a,ll b,ll &x,ll &y) {
	if(b==0) {
		x=1,y=0;
		return;
	}
	Exgcd(b,a%b,y,x),y-=a/b*x;
}
ll Inv(int a,int P) {
	ll x,y;
	Exgcd(a,P,x,y);
	return (x%P+P)%P;
}

struct SolveP{
	int C[N][N];
	int F[N],G[N];
	int A[N],B[N];
	int X[N],Y[N];
	int P,I2;
	void Init(int x) { 
		P=x; 
		rep(i,0,n) rep(j,C[i][0]=1,i) C[i][j]=(C[i-1][j-1]+C[i-1][j])%P;
		I2=(P+1)/2;
	}
	int Solve(int m) {
		if(P==1) return 0;
		int l1=(n-1)/m+1,l2=l1-1;
		int c1=0,c2=0;
		rep(i,1,m) if((n-i)/m+1==l1) c1++;
		else c2++;
		int Inv=dp[l1][1]==1?1:I2;
		rep(i,1,l1) A[i-1]=1ll*J[i-1]*dp[l1][i]%P*Inv%P;
		Inv=dp[l2][1]==1?1:I2;
		rep(i,1,l2) B[i-1]=1ll*J[i-1]*dp[l2][i]%P*Inv%P;
		// 将A,B偏移补充常数项
		// 同时除掉常数项，为下面做除法铺路

		int d=c1+c2;
		// A,B存储偏移之后的值，d为偏移量
		// X,Y存储除法之后的值
		F[0]=X[0]=Y[0]=1;
		rep(i,1,n-d) {
			ull x=0,y=0;
			// 注意这里计算的是两边次数为x^{i-1}一项的值
			rep(j,1,min(l1-1,i)) {
				// 将除法的结果乘上求导以后的值，注意求导以后第一位消失了
				x+=1ll*X[i-j]*A[j]%P*C[i-1][j-1];
				(j&15)==0 && (x%=P);
				// 求导以后是j-1位，因此实际应该是x^{i-j}*x^{j-1}
			}
			rep(j,1,min(l2-1,i)) {
				y+=1ll*Y[i-j]*B[j]%P*C[i-1][j-1];
				(j&15)==0 && (y%=P);
			}
			// 由[x^{i-1}]H'(x)一项得到[x^i]H(x)
			F[i]=X[i]=Y[i]=(x%P*c1+y%P*c2)%P;
			// 接下来做二项除法(雾)
			x=0,y=0;
			rep(j,1,min(i,l1-1)) {
				x+=1ll*(P-A[j])*X[i-j]%P*C[i][j];
				(j&15)==0 && (x%=P);
			}
			rep(j,1,min(i,l2-1)) {
				y+=1ll*(P-B[j])*Y[i-j]%P*C[i][j];
				(j&15)==0 && (y%=P);
			}
			X[i]=(X[i]+x)%P,Y[i]=(Y[i]+y)%P;
		}
		int ans=0;
		rep(i,0,n-d) {
			F[i]=1ll*F[i]*C[i+d][d]%P*J[d]%P;
			ans=(ans+(((n-i-d)&1)?-1:1)*F[i])%P;
		}
        // 将除掉的系数乘回来
		rep(i,1,c1) ans=1ll*ans*dp[l1][1]%P;
		rep(i,1,c2) ans=1ll*ans*dp[l2][1]%P;
		ans=(ans%P+P)%P;
		return ans;
	}
} Sol2;

int t;
void Init() {
	t=1;
	for(t=1;P%2==0;) t*=2,P/=2;
	Sol1.Init(t),Sol2.Init(P);
}

void Solve(int m) {
	int x=Sol1.Solve(m),y=Sol2.Solve(m);
    // CRT
	ll res=1ll*((y-x)%P+P)*Inv(t,P)%P;
	ll mod=t*P;
	res=((res*t+x)%mod+mod)%mod;
	printf("%lld\n",res);
}

int main() {
	freopen("fate.in","r",stdin),freopen("fate.out","w",stdout);
	n=rd(),m=rd(),P=rd();
	rep(i,J[0]=1,n) J[i]=1ll*J[i-1]*i%P;
	dp[0][0]=S[0]=1;
	rep(i,1,n) {
		drep(j,i,1) {
			dp[i][j]=(S[j-1]*2ll+P-dp[i-1][j-1])%P;
			S[j]+=dp[i][j],Mod1(S[j]);
		}
	}
	Init();
	rep(i,1,m) Solve(rd());
}