[BJ United Round 3] 押韵
[BJ United Round #3] 押韵
先%%%%%%%%%%%%%%%%% EI
下文默认模数为$P$
简要题意:求:用$k$种元素,每种元素使用$d$的倍数次,排成一个长度为$nd$的序列 的方案数
这个题目的设定就让人想到两个离不开的元素 : (模数暗示了?)
指数型生成函数 + 单位根反演
显然可以得到每一种元素的指数型生成函数为
$\begin{aligned} \text{EGF(Element)}=F(x)=\sum_{d|i} \frac{x^i} {i!}\end{aligned}$带入单位根反演$\begin{aligned}\ [d|n]=\frac{\sum_0^{d-1} \omega_d^{in} } {d}\end{aligned}$
即$F(x)=\begin{aligned}\frac{1} {d}\cdot \sum_{i=0}^{d-1}e^{\omega_d^ix}\end{aligned}$
而总的生成函数就是 $G(x)=F^k(x)$
即$\begin{aligned} G(x)=\frac{1} {d^k}\cdot (\sum_{i=0}^{d-1}e^{\omega_d^ix})^k\end{aligned}$
其中的和式幂次展开会得到一个$k^d$项的多项式,我们要求$[x^n]G(x)$,就需要展开得到每一项的幂系数
所以显然我们需要先合并同类项一下。。。
而幂系数是一个单位根之和的形式,这就需要我们寻找单位根之间的关系
这里得到一个思路:用$d$次单位根中的$\varphi(d)$个作为基底,以简单的 有理数/整系数 表示出所有的$\omega_d^i$
对于$d=4$的情况比较简单,$\varphi(d)=2$,可以得到四个单位根分别为$1,\omega,-1,-\omega$
可以枚举得到的和为$x+y\omega$,然后求系数
优先考虑组合意义,可以发现就是在平面上每次可以走四个方向,$k$步之后最终到达$(x,y)$的方案数
两个维度分立的情况,还需要枚举每个维度走了几步,所以用一种巧妙的转化两个维度联系在一起
将平面旋转$\frac{\pi} {8}$,并且扩大$\sqrt 2$倍,得到新的坐标为$(x-y,x+y)$,新的行走方向是$(+1,+1),(-1,-1),(-1,+1),(+1,-1)$
这样以来,每次每个维度都有行走,可以确定每个维度$+1$和$-1$的次数,直接组合数排列即可得到答案
对于$d=6$,甚至是更一般的情况的情况
只在代数层面来看单位根似乎十分抽象,不如从复平面单位根上找一找灵感
下面是$d=6$的情形
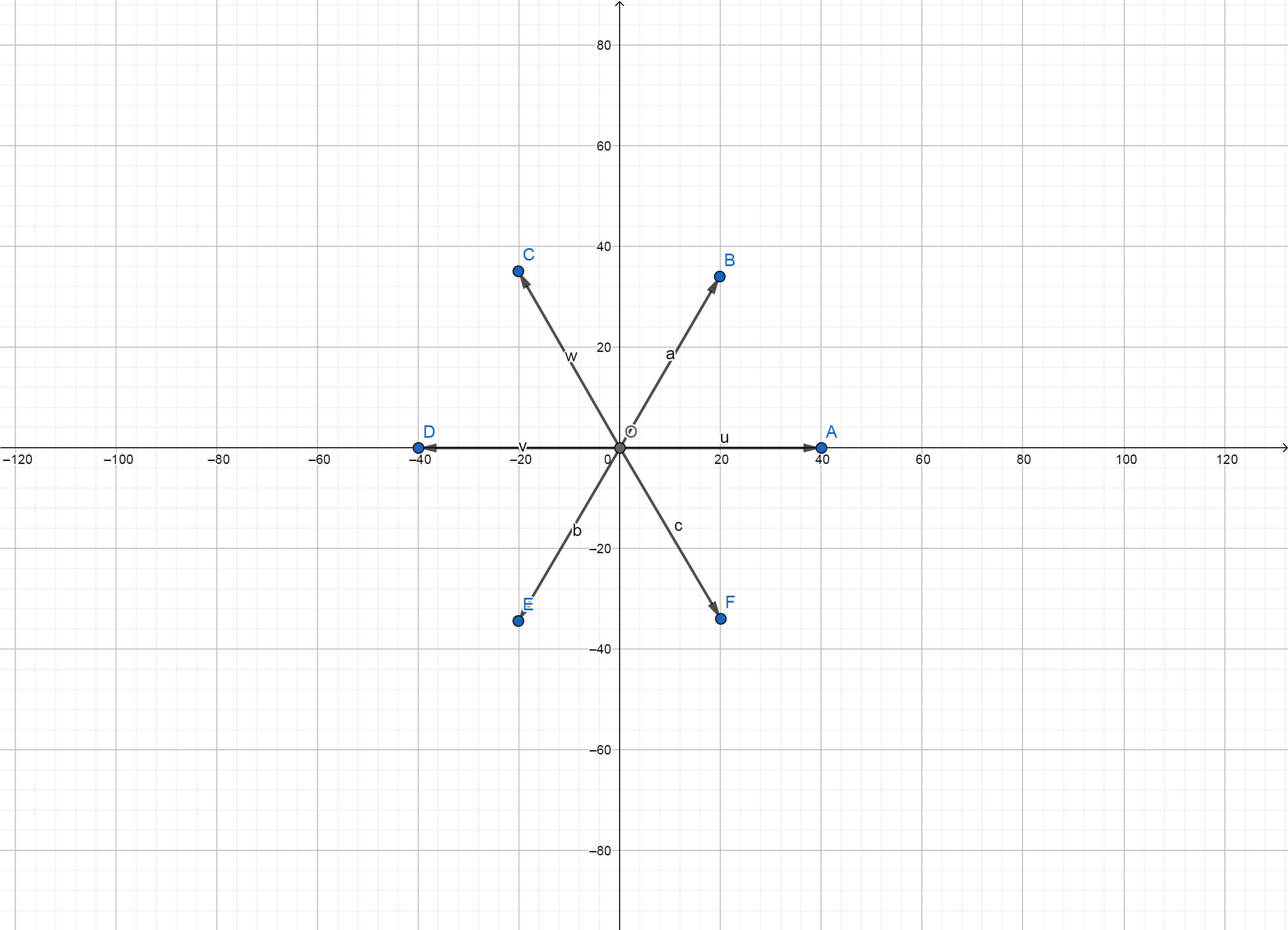
$\varphi(6)=2$,假设以$\overrightarrow{OA},\overrightarrow{OB}$作为基底,可以直观地得到基底表达
| $\overrightarrow{OA}=1$ | $\overrightarrow{OB}=\omega$ | |
|---|---|---|
| $\overrightarrow{OA}=\omega_6^0$ | 1 | 0 |
| $\overrightarrow{OB}=\omega_6^1$ | 0 | 1 |
| $\overrightarrow{OC}=\omega_6^2$ | -1 | 1 |
| $\overrightarrow{OD}=\omega_6^3$ | -1 | 0 |
| $\overrightarrow{OE}=\omega_6^4$ | 0 | -1 |
| $\overrightarrow{OF}=\omega_6^5$ | 1 | -1 |
由此我们得到了一个$\varphi(d)$维数的表达方法
把每一维看做不同元,也就是说,得到了一个$\varphi(d)$维,$O(1)$次的多项式,需要我们求高维多项式幂次
令$N=k^{\varphi(d)}$
直接压位暴力多项式复杂度为$O(N\log N-N\log^2N)$,而且面临着模数难以处理,常数大的问题
所以$\text{EI}$又用出了一个巧妙的暴力方法解决这个问题,以$d=6$为例,先做一下处理,得到要求的多项式
似乎每次$k$次幂总是求导+递推?
$f(x,y)=x^2y+xy^2+y^2+y+x+x^2,g(x,y)=f^k(x,y)$
$g(x,y)$对于$x$求偏导,得到$g’(x,y)=kf^{k-1}(x,y)f’(x,y)$
即$g’(x,y)f(x,y)=kg(x,y)f’(x,y)$
$f’(x,y)=2xy+2x+y^2+1$
然后我们要解这个方程,考虑乘积为$[x^ny^m]$一项两边的系数
左边$=[x^{n-2}y^{m-1}]+[x^{n-1}y^{m-2}]+[x^{n}y^{m-2}]+[x^{n}y^{m-1}]+[x^{n-1}y^{m}]+[x^{n-2}y^{m}]$
换成$g(x,y)$的系数应该是
左边$=(n-1)[x^{n-1}y^{m-1}]+n[x^{n}y^{m-2}]+(n+1)[x^{n+1}y^{m-2}]+(n+1)[x^{n+1}y^{m-1}]+n[x^{n}y^{m}]+(n-1)[x^{n-1}y^{m}]$
右边$=2k[x^{n-1}y^{m-1}]+2k[x^{n-1}y^m]+k[x^ny^{m-2}]+k[x^ny^m]$
其中$[x^{n+1}y^{m-1}]$只出现了一次,按照先$n$递增再$m$递增的顺序进行递推,即
$\begin{aligned}\ [x^ny^m]=\frac{2k[x^{n-2}y^{m}]+2k[x^{n-2}y^{m+1}]+k[x^{n-1}y^{m-1}]+k[x^{n-1}y^{m+1}]} {n}\end{aligned}$ $\begin{aligned}-\frac{(n-2)[x^{n-2}y^{m}]+(n-1)[x^{n-1}y^{m-1}]+n[x^{n}y^{m-1}]+(n-1)[x^{n-1}y^{m+1}]+(n-2)[x^{n-2}y^{m+1}]} {n}\end{aligned}$边界条件是 $\begin{aligned}\ [x^i]=[y^i](i\ge k)=\binom{k} {i-k}\end{aligned}$ (由系数$x,x^2$或$y,y^2$得到)
由此带入递推即可
综上,得到的每项的系数的复杂度为$O(d\cdot k^{\varphi(d)})$ ,其中$d$为递推每项需要的时间
由系数得到答案仍然需要一次快速幂,因此依然带一个$\log P$
1 |
|

