平面图的欧拉定理

平面图

平面图是一张无向图，顾名思义

存在一种在平面上画点的方法，使得所有的边不会相交

欧拉定理

对于一张平面图$G=(V,E)$，$F$为平面图上的边把平面划分的区域个数（注意统计最外层的无限区域），则

一张平面图是连通的 $\Longleftrightarrow$ $|V|-|E|+|F|=2$

下面是一个例子

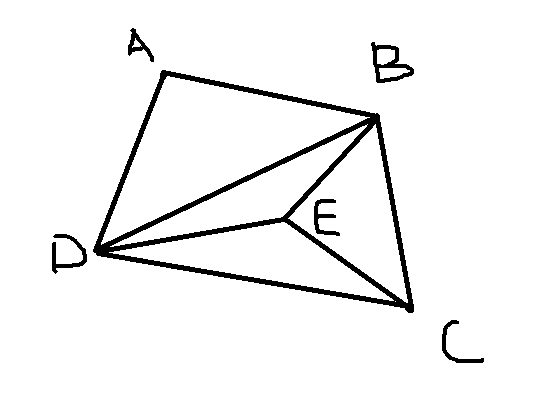
$|V|=5,|E|=8,F=5$ (包含最外层的区域)

很显然这个定理也可以用来统计联通块的数量/区域的数量

即$C=|V|-|E|+|F|-1$

欧拉定理与网格图

当题目涉及到网格图染色问题时，不妨将所有染色的网格视为点，边即为四联通

此时构成一个特殊的平面图，且此时可以发现

$F$为 4相邻块个数 + 空腔个数 + 1

$|E|$为相邻对数

$|V|$为染色个数

由此可以在染色问题上把 空腔数量 与 连通性结合起来

作为一种可能出现的思路