CF1491G - Switch and Flip

题目大意

有$n$个硬币，编号$1-n$，第$i$个位置上当前放了编号$a_i$的硬币

每次交换$(a_i,a_j)i\ne j$，且将硬币$a_i,a_j$翻转

求方案使得最终使得$a_i=i$且每个硬币恰好为原先方向

$n\ge 3$，方案步数$\leq n+1$


分析

显然要先对于$a_i$求出置换环，步数$\leq n+1$说明

1.general的情况可以用$n$步解决$n$个点

2.存在至多一个特殊情况要$n+1$步

手玩发现我们无法$n$步解决一个大小为$n$的环

但是如果环上恰好已经有两个硬币被翻过，那么可以

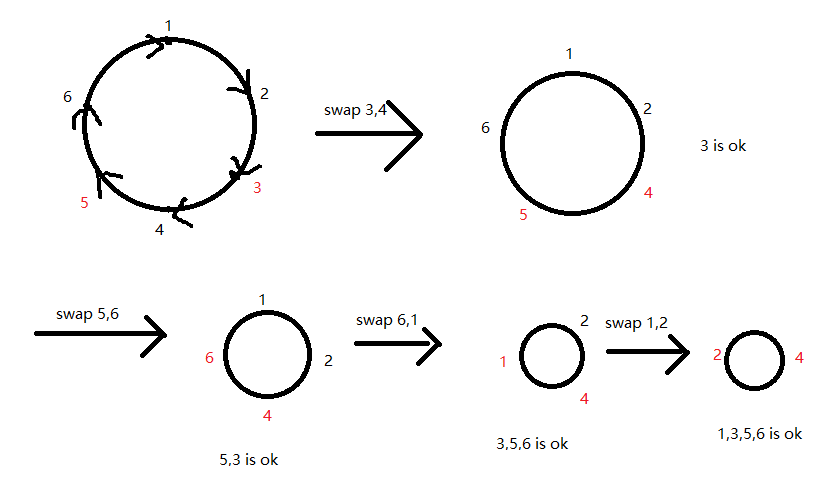
QQ截图20210511180918.png

图上点表示硬币编号，箭头所指是这个硬币应该在的位置

我们从一个已经翻转的点开始，不断交换$i,a_i$上的硬币，会将$a_i$移动到到应该在的位置上

同时下一个位置被翻转

不断进行这个操作，直到这个点消去了半边环，遇到了下一个点也是被翻过的点

此时再从下一个点开始将环的另外半边消去


那么考虑如何让一个环有两个已经翻转的点

假设提取出了$c$个环，我们可以先尽量成对匹配两个环

通过一次跨过环的交换操作合并两个大小$x,y$的环，同时生成两个翻转点

然后进项上面的操作，需要$x+y-1$次，恰好一共$x+y$次


那么对于最后剩下的一个环

1.如果前面已经有环被匹配过

那么随便选择一个当前$a_i=i$的自环与其合并即可


2.整个图为一个大环

先通过交换$1,a_1$将$a_1$弹出，然后$a_1$再和环上另外一个元素交换

此时$a_1$变成未翻转状态，环又并成一个环+2个翻转点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
const int N=2e5+10,INF=1e9+10;

int n;
int a[N],vis[N],b[N],c;

int X[N],Y[N],C,col[N];
void Swap(int x,int y){
	X[++C]=x,Y[C]=y;
	swap(a[x],a[y]),col[a[x]]^=1,col[a[y]]^=1;
}
void Solve(int i){ 
	while(!col[a[i]]) i=a[i];
	while(!col[a[a[i]]]) Swap(i,a[i]);
	i=a[i];
	while(i!=a[i]) Swap(i,a[i]);
}

int main(){
	n=rd();
	rep(i,1,n) a[i]=rd();
	rep(i,1,n) if(!vis[i]) {
		for(int j=i;!vis[j];j=a[j]) vis[j]=1;
		b[++c]=i;
	}
	for(int i=1;i<c;i+=2) {
		Swap(b[i],b[i+1]);
		Solve(b[i]);
	}
	if(c&1) {
		if(c==1) {
			int t=a[1];
			Swap(1,a[1]),Swap(t,a[1]);
			Solve(i);
		} else {
			rep(i,1,n) if(a[i]==i) {
				Swap(i,b[c]);
				Solve(i);
				break;
			}
		}
	}
	printf("%d\n",C);
	rep(i,1,C) printf("%d %d\n",X[i],Y[i]);
}