CF1503E - 2-Coloring

题目大意

给定一个$n\times m$网格图，给每个格子黑白染色，使得最终

每行恰好只有一条黑色线段，每列恰好只有一条白色线段

求方案数


分析

这种东西当然是分析好情况就ok了

大概分几种情况

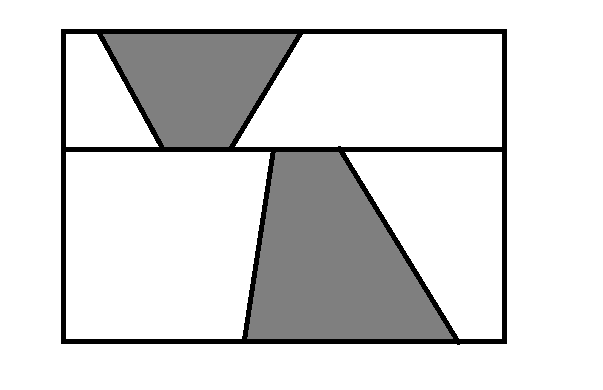
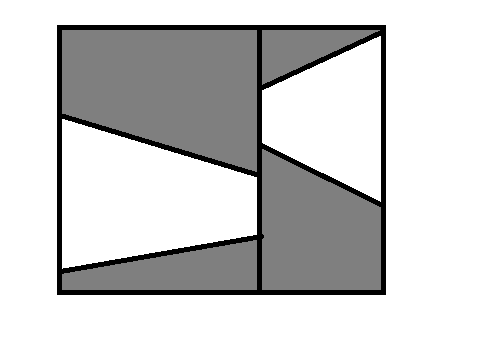
1.QQ截图20210512171601.png

2.QQ截图20210512171647.png

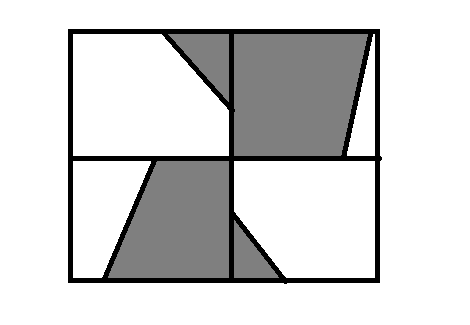
3.QQ截图20210512175626.png

为什么要把第三种拿出来说呢，实际上第三种是1和2的交（黑白都是梯形，确信）

那么枚举中间的分界线，根据中间相距最近的两个点的位置就能用组合数确定答案

（虽然代码里不是组合数）

前缀和优化即可$O(nm)$，注意两个梯形可以对称，所以最后答案*2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

const int N=2030,INF=1e9+10,P=998244353;

int n,m;
int dp[N][N],ans;
// dp[i][j]是i个，每个>=0且递增，最后一个<=j的方案数
ll F(int n,int m){
	if(m<0) return 0;
	return m==0?1:(dp[n][m]-dp[n][m-1]+P)%P;
}
int S[N],T[N];

void Calc(){
	rep(i,1,n-1) {
		int s=0;
		rep(j,1,m-1) {
			s=(s+1ll*F(j,i)*dp[m-j][i-1])%P;
			ans=(ans+1ll*s*F(m-j,n-i)%P*dp[j][n-i-1])%P;
		}
	}
}

int main(){
	dp[0][0]=1;
	rep(i,1,N-1){
		rep(j,0,N-1) {
			if(j) dp[i-1][j]+=dp[i-1][j-1],Mod1(dp[i-1][j]);
			dp[i][j]=dp[i-1][j];
		}
	}
	n=rd(),m=rd();
	Calc(),swap(n,m),Calc();
	rep(i,1,n-1) {
		int s=0;
		rep(j,1,m-1) {
			s=1ll*F(j,i)*dp[m-j][i-1]%P;
			ans=(ans-1ll*s*F(m-j,n-i)%P*dp[j][n-i-1])%P;
		}
	}
	Mod2(ans);
	printf("%d\n",ans*2%P);
}